Question

How many different ways can the letters of grade be arranged?

( I have to use permutation to solve please and thank you )

Answer 1

120 ways

Step-by-step explanation:

The given word is :

• GRADE
• It has five letters

⇒ Any of the 5 letters can be in each place

⇒ 5! ways is the number

⇒ 5 x 4 x 3 x 2 x 1

⇒ 20 x 6

⇒ 120 ways

Answer 2

Answer: 120 different ways

Step-by-step explanation:

Assuming you want to arrange the letters of "grade", then we have 5 unique letters. That gives 5! = 5*4*3*2*1 = 120 different permutations. Order matters. The exclamation mark means factorial. It means we start at 5 and count our way down to 1, multiplying along the way.

In other words, we have 5 choices for the first slot, then 4 choices for the next slot, and so on. We count down because we cannot reuse any previously selected letter.

Alternatively, you can use the nPr permutation formula

`_nP_r = (n!)/((n-r)!)`

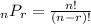
where n = 5 and r = 5 since we have 5 letters to pick from and 5 slots to fill.