Question

2. An investment of $200 is now valued at $315. Assuming continuous compounding has

occurred for 6 years, approximately what interest rate is needed to be for this to be
possible?

Answer 1

An yearly interest rate of 7.57% is needed to be for this to be possible.

Explanation:

The amount of money after t years of continuous compounding is given by:

`P(t) = P(0)e^(rt)`

In which P(0) is the initial investment and r is the interest rate, as a decimal.

In this problem, we have that:

`P(0) = 200, P(6) = 315`

We have to find r.

`P(t) = P(0)e^(rt)`

`315 = 200e^(6r)`

`e^(6r) = (315)/(200)`

`\ln{e^(6r)} = \ln{(315)/(200)}`

`6r = \ln{(315)/(200)}`

`r = \frac{\ln{(315)/(200)}}{6}`

`r = 0.0757`

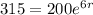
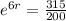
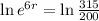
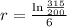
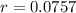
An yearly interest rate of 7.57% is needed to be for this to be possible.