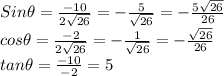Answer:
STEP 3
Explanation:
Francesca drew point (–2, –10) on the terminal ray of angle
 , which is in standard position. She found values for the six trigonometric functions using the steps below.
, which is in standard position. She found values for the six trigonometric functions using the steps below.
Step 1
A unit circle is shown. A ray intersects point (negative 2, negative 10) in quadrant 3. Theta is the angle formed by the ray and the x-axis in quadrant 1.
Step 2

Step 3
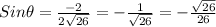
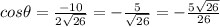
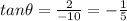

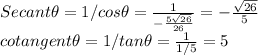
Francesca made her first error in step 3 because the sine, cosine, and tangent ratios are incorrect, which also resulted in incorrect cosecant, secant, and tangent functions.
The correct values are: