Question

Ryan is driving home from work and notices a deer leaping onto the road about 25 m in front of his car. He immediately applies the brakes, which causes him to skid. Luckily his speed was only 60 km/h before applying the brakes. If the mass of his car is 1490 kg, what coefficient of friction must exist between the tires and the road to stop the car in 25 m?

Answer 1

mu = 0.56

Step-by-step explanation:

The friction force is calculated by taking into account the deceleration of the car in 25m. This can be calculated by using the following formula:

`v^2=v_0^2+2ax\\`

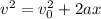
v: final speed = 0m/s (the car stops)

v_o: initial speed in the interval of interest = 60km/h

= 60(1000m)/(3600s) = 16.66m/s

x: distance = 25m

BY doing a the subject of the formula and replace the values of v, v_o and x you obtain:

`a=(v^2-v_o^2)/(2x)=(0m^2/s^2-(16.66m/s)^2)/(2(25m))=-5.55(m)/(s^2)`

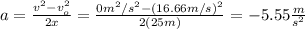
with this value of a you calculate the friction force that makes this deceleration over the car. By using the Newton second's Law you obtain:

`F_f=ma=(1490kg)(5.55m/s^2)=8271.15N`

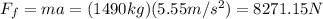
Furthermore, you use the relation between the friction force and the friction coefficient:

`F_f= \mu N=\mu mg\\\\\mu=(F_f)/(mg)=(8271.15N)/((1490kg)(9.8m/s^2))=0.56`

hence, the friction coefficient is 0.56