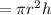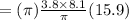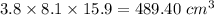Answer:
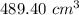
Explanation:
Given:
The given two cross-sections have the same area such that the heights of the two solids are equal.
To find: volume of the cylinder
Solution:
Let r represents the radius of the cylinder.
Area of the cross-section of the cylinder ( i.e., area of a circle) = area of the cross-section of the other solid (are of the rectangle)
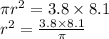
Height of the cylinder (h) = 15.9 cm
Volume of the cylinder