Question

Convert (1, 1) to polar form.

OA (2, 45°)
OB. (1,45°)
OC. (2,225)
OD. (2.459)

Answer 1

Answer: Choice D

`(√(2){, 45^(\circ))`

============================================================

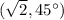
Step-by-step explanation:

The original point is in cartesian form (x,y). We have x = 1 and y = 1 pair up together.

The radius is
`r = √(x^2+y^2) = √(1^2+1^2) = √(2)`

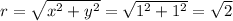
The angle theta is
`\theta = \tan^(-1)(y/x) = \tan^(-1)(1/1) = 45^(\circ)`

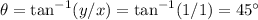
Therefore, the polar form is
`(r, \theta) = (√(2), 45^(\circ))`

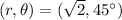
The idea is to start at the origin while facing directly east at the angle 0 degrees. Then turn 45 degrees to the north (going counterclockwise) and then move
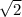`√(2)` units away from the origin. Doing these steps will take you to the point (x,y) = (1,1)