Question

A researcher wishes to estimate the percentage of adults who support abolishing the penny. What size sample should be obtained if he wishes the estimate to be within 2 percentage points with 99​% confidence if ​(a) he uses a previous estimate of 25​%? ​(b) he does not use any prior​ estimates?

Answer 1

a) We need a sample size of at least 3109.

b) We need a sample size of at least 4145.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

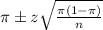
In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

The margin of error is:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

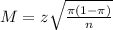
99% confidence level

So
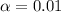`\alpha = 0.01`, z is the value of Z that has a pvalue of
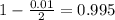`1 - (0.01)/(2) = 0.995`, so
`Z = 2.575`.

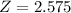(a) he uses a previous estimate of 25​%?

we need a sample of size at least n.

n is found when
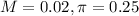`M = 0.02, \pi = 0.25`. So

`M = z\sqrt{(\pi(1-\pi))/(n)}`

`0.02 = 2.575\sqrt{(0.25*0.75)/(n)}`

`0.02√(n) = 2.575√(0.25*0.75)`

`√(n) = (2.575√(0.25*0.75))/(0.02)`

`(√(n))^(2) = ((2.575√(0.25*0.75))/(0.02))^(2)`

`n = 3108.1`

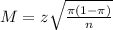
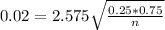
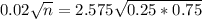
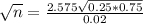
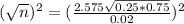
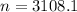
We need a sample size of at least 3109.

(b) he does not use any prior​ estimates?

When we do not use any prior estimate, we use
`\pi = 0.5`

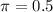
So

`M = z\sqrt{(\pi(1-\pi))/(n)}`

`0.02 = 2.575\sqrt{(0.5*0.5)/(n)}`

`0.02√(n) = 2.575√(0.5*0.5)`

`√(n) = (2.575√(0.5*0.5))/(0.02)`

`(√(n))^(2) = ((2.575√(0.5*0.5))/(0.02))^(2)`

`n = 4144.1`

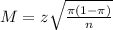
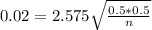
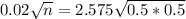
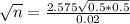
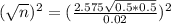
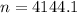
Rounding up

We need a sample size of at least 4145.