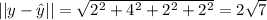Answer:
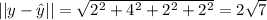
Explanation:
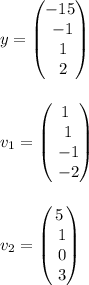
And according to the information given the closest point to
 in W is
in W is
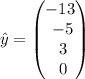
This is a problem when they give you more information than you actually need, by definition the distance from a vector to a subspace is given as the distance to the closest vector of the subspace, usually you have to find the vector using the Gram-Schmidt process and the orthogonal projection of the vector to the subspace, for this case you do not need any of that because the vector is given so all you find is the distance between
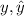 which is
which is