Given:
Let us assume that E,F,G,H be the points at which the circle touches the line segment AB, BC, CD, DA.
The length of EB = 9.6 units.
The length of AH = 3.7 units.
The length of CD = 12 units.
We need to determine the perimeter of ABCD.
Lengths of sides of the quadrilateral ABCD:
Let CG = x, then DG = 12 - x
We know the property the property that "if the lengths of the two tangents drawn from an exterior point to a circle are equal".
Hence, applying the property, we have;
AH = AE = 3.7 units.
EB = BF = 9.6 units.
CG = CF = x units.
DG = DH = (12 - x) units.
Perimeter of quadrilateral ABCD:
The perimeter of ABCD can be determined by adding all the lengths of the sides of the quadrilateral ABCD.
Thus, we have;
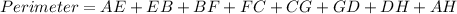
Substituting the values, we have;
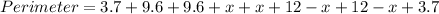
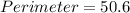
Thus, the perimeter of the quadrilateral ABCD is 50.6 units.