Question

An ordinary (fair) die is a cube with the numbers 1 through 6 on the sides (represented by painted spots). Imagine that such a die is rolled twice in succession and that the face values of the two rolls are added together. This sum is recorded as the outcome of a single trial of a random experiment.

Compute the probability of each of the following events.
Event A: The sum is greater than 5.
Event B: The sum is an even number.
Write your answers as exact fractions.

Answer 1

The probability of event A is
`(7)/(11)`.

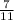The probability of event B is
`(6)/(11)`.

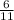Explanation:

The sample space of rolling a fair six-sided dice is as follows:

S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)

(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

Now consider the experiment of the computing the sum of the two rolls as follows:

X = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

Number of total outcomes, N = 11.

The probability of an event E is the ratio of the number of favorable outcomes to the total number of outcomes.

`P(E)=(n(E))/(N)`

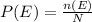
The event A is defined as the sum is greater than 5.

The sample space of A is:

A = {6, 7, 8, 9, 10, 11, 12}

n (A) = 7

Compute the probability of event A as follows:

`P(A)=(n(A))/(N)=(7)/(11)`

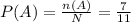
Thus, the probability of event A is
`(7)/(11)`.

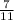The event B is defined as the sum is an even number.

The sample space of B is:

B = {2, 4, 6, 8, 10, 12}

n (B) = 6

Compute the probability of event B as follows:

`P(B)=(n(B))/(N)=(6)/(11)`

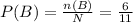
Thus, the probability of event B is
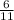`(6)/(11)`.