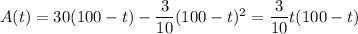Question

A large tank is filled to capacity with 600 gallons of pure water. Brine containing 5 pounds of salt per gallon is pumped into the tank at a rate of 6 gal/min. The well-mixed solution is pumped out at a rate of 12 gallons/min. Find the number A(t) of pounds of salt in the tank at time t. A(t)

Answer 1

Salt flows into the tank at a rate of

(5 lb/gal) * (6 gal/min) = 30 lb/min

The volume of solution in the tank after t min is

600 gal + (6 gal/min - 12 gal/min)*(t min) = 600 - 6t gal

which means salt flows out at a rate of

(A(t)/(600 - 6t) lb/gal) * (12 gal/min) = 2 A(t)/(100 - t) lb/min

Then the net rate of change of the salt content is modeled by the linear differential equation,

`A'(t)=30-(2A(t))/(100-t)`

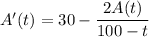
Solve for A:

`A'+(2A)/(100-t)=30`

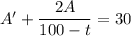
Multiply both sides by the integrating factor,
`\frac1{(100-t)^2}`:

`(A')/((100-t)^2)+(2A)/((100-t)^3)=(30)/((100-t)^2)`

`\left(\frac A{(100-t)^2}\right)'=(30)/((100-t)^2)`

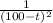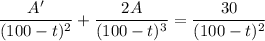
Integrate both sides:

`\frac A{(100-t)^2}=(30)/(100-t)+C`

`\implies A(t)=30(100-t)+C(100-t)^2`

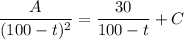
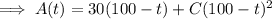
The tank starts with no salt, so A(0) = 0 lb. This means

`0=30(100)+C(100)^2\implies C=-\frac3{10}`

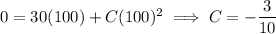
and the particular solution to the ODE is

`A(t)=30(100-t)-\frac3{10}(100-t)^2=\frac3{10}t(100-t)`