Question

In a game a player draws and replaces a card from a deck 2 times. The possible outcomes and payouts are shown. What is the

expected value for someone playing the game?
**plz help me***

Answer 1

Given:

Given that in a game a player draws and replaces a card from a deck 2 times.

The possible outcomes and payouts are given.

We need to determine the expected value for someone playing the game.

Expected value:

The expected value for someone playing the game can be determined by

`EV=((26)/(52))(\$ 20)+((52)/(52))(\$4)+((52)/(52))(\$ 0)+((26)/(52))(-\$12)`

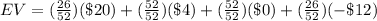
Simplifying the values, we have;

`EV=((1)/(2))(\$ 20)+(1)(\$4)+(1)(\$ 0)+((1)/(2))(-\$12)`

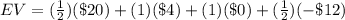
Dividing the terms, we get;

`EV=\$ 10+\$4+\$ 0+-\$6`

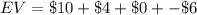
Adding, we have;

`EV=\$ 8`

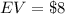
Thus, the expected value for someone playing the game is $8