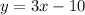Question

The line on the graph passes through to points A (1, 3) B (7, 1)

Answer 1

a. Gradient of line AB is
`-(1)/(3)`

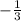
b. The gradient of a line perpendicular to line AB is 3

c. The equation of a line passing through point (4,2) and perpendicular to AB is
`y = 3x - 10`

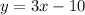
Explanation:

a.

Given

Point A (1, 3) B (7, 1)

Required

Gradient of AB

Gradient of a line is represented by m

m is calculated using the following formula

`m = (y_(2) - y_(1) )/(x_(2) - x_(1))`

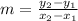
Where the general representation of the coordinates are
`A(x_1,y_1) and B(x_2,y_2)`

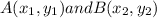
From the given data, we have that

`A(x_1,y_1) = A(1,3)`

`B(x_2,y_2) = A(7,1)`

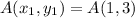
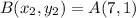
So, from there we know that

`x_1 = 1;y_1 =3; x_2 = 7;y_2 =1`

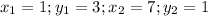
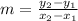`m = (y_(2) - y_(1) )/(x_(2) - x_(1))` becomes

`m = (1 - 3)/(7 - 1)`

`m = (-2)/(6)`

`m = -(1)/(3)`

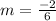
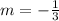
b.

Required

Find the gradient of a line perpendicular to AB

Recall that gradient of a line is represented by m

The condition for perpendicularity is that
`m_1.m_2 = -1`

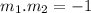
In (a) above, we solved the gradient of line AB to be
`-(1)/(3)`

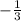
Let
`m_1` represent gradient of line AB

Hence,
`m_1 = -(1)/(3)`

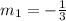
Substitute
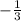`-(1)/(3)` for
`m_1` in
`m_1.m_2 = -1`

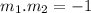
This will give

`(-1)/(3) * m_2 = -1`

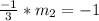
Multiply both sides by -3

`-3 * (-1)/(3) * m_2 = -1 * -3`

`m_2 = -1 * -3`

`m_2 = 3`

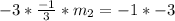
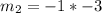
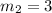
Hence, the gradient of a line perpendicular to line AB is 3

c.

Required

Find the equation of a line passing through point (4,2) and perpendicular to AB

Equation is calculated using the gradient formula

`m = (y_(2) - y_(1) )/(x_(2) - x_(1))`

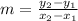
Since only one point is known, the formula is represented as follows

`m = (y - y_(1) )/(x - x_(1))`

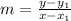
Where
`x_1 = 4; y_1 = 2`

Since, the line is perpendicular to line AB, then its gradient m is equal to 3 (as calculated in b above)

So, we have
`x_1 = 4; y_1 = 2; m = 3`

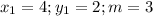
By substitution

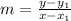`m = (y - y_(1) )/(x - x_(1))` becomes

`3 = (y - 2)/(x - 4)`

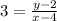
Multiply both sides by x - 4

`3 * (x - 4) = (y - 2)/(x - 4) * (x - 4)`

`3(x - 4) = {y - 2}`

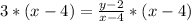
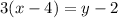
Open brackets

`3x - 12 = y - 2`

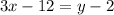
Make y the subject of formula

`3x - 12 + 2= y`

`3x - 10 = y`

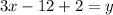
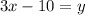
Reorder

`y = 3x - 10`

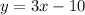
Hence, the equation of a line passing through point (4,2) and perpendicular to AB is
`y = 3x - 10`