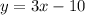Answer:
a. Gradient of line AB is
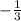
b. The gradient of a line perpendicular to line AB is 3
c. The equation of a line passing through point (4,2) and perpendicular to AB is
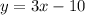
Explanation:
a.
Given
Point A (1, 3) B (7, 1)
Required
Gradient of AB
Gradient of a line is represented by m
m is calculated using the following formula
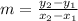
Where the general representation of the coordinates are
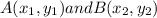
From the given data, we have that
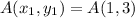
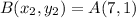
So, from there we know that
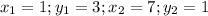
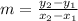 becomes
becomes
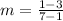
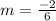
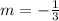
b.
Required
Find the gradient of a line perpendicular to AB
Recall that gradient of a line is represented by m
The condition for perpendicularity is that
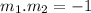
In (a) above, we solved the gradient of line AB to be
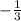
Let
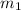 represent gradient of line AB
represent gradient of line AB
Hence,
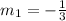
Substitute
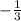 for
for
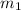 in
in
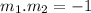
This will give
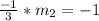
Multiply both sides by -3
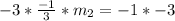
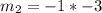
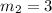
Hence, the gradient of a line perpendicular to line AB is 3
c.
Required
Find the equation of a line passing through point (4,2) and perpendicular to AB
Equation is calculated using the gradient formula
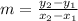
Since only one point is known, the formula is represented as follows
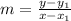
Where
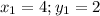
Since, the line is perpendicular to line AB, then its gradient m is equal to 3 (as calculated in b above)
So, we have
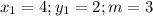
By substitution
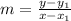 becomes
becomes
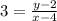
Multiply both sides by x - 4
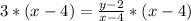
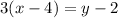
Open brackets
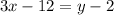
Make y the subject of formula
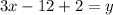
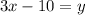
Reorder
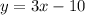
Hence, the equation of a line passing through point (4,2) and perpendicular to AB is