Question

Boys and Girls Club of America wants to determine the proportion of Big Brothers who have seen The Matrix. If the proportion differs from 40%, then the organization has decided that it will file for bankruptcy. Suppose a hypothesis test is conducted and the test statistic is -1.89. If α = 0.45, what is the most appropriate decision and reasoning?

Group of answer choices

Don’t file for bankruptcy because the p-value is not smaller than α.

File for bankruptcy because the p-value is smaller than α.

Don’t file for bankruptcy because the p-value is smaller than α.

File for bankruptcy because the p-value is not smaller than α.

Answer 1

Correct option:

File for bankruptcy because the p-value is smaller than α.

Explanation:

The Boys and Girls Club of America wants to determine the proportion of Big Brothers who have seen The Matrix.

The organization would file for bankruptcy if the proportion of Big Brothers who have seen The Matrix is different from 40%.

The hypothesis to test whether the organization would file for bankruptcy is:

H₀: The organization would not file for bankruptcy, i.e. p = 0.40.

Hₐ: The organization would file for bankruptcy, i.e. p ≠ 0.40.

The z-test for single proportion is used to perform the test.

The test statistic is, z = -1.89.

The significance level of the test is, α = 0.45.

Compute the p-value of the test as follows:

`p-value=2* P(Z<-1.89)\\=2* 0.02938\\=0.05876`

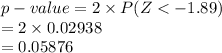
*Use a z-table.

Decision rule:

If the p-value is less than the significance level of the test then the null hypothesis will be rejected and vice-versa.

p-value = 0.05876 < α = 0.45.

The null hypothesis will be rejected.

Thus, it can be concluded that the organization would file for bankruptcy since the p-value of the test is less than the significance level.