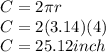Question

A circular sign is precisely designed to have an area of 50.24 square inches. What is the sign's circumference?

Answer 1

Explanation:

First of all we need to know the formula for the circumference which is:
`c=2\pi r`

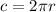
We don't have the radius. What we only have is the area; therefore, we must use the area formula and extract the radius from it.

The formula for the area is:
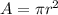`A=\pi r^2` Solve for r;

`r^2=(A)/(\pi)\\ r=\sqrt[]{(A)/(\pi) }`

`r=\sqrt[]{(50.24inch^2)/(3.14) }`

`r=\sqrt[]{16inch^2}\\ r=4inch`

Now that we've found the radius, we simply plug it into the circumference formula.

`C=2\pi r\\C=2(3.14)(4)\\C=25.12inch`