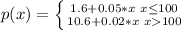Answer:
a) The revenue function, in $, is given by
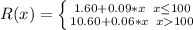
b) The profit function is $ is given by
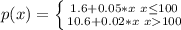
Explanation:
a) For a value of x less than or equal to 100, we have that the revenue function (in $) is
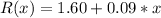 .
.
For x = 100 therefore, we have that
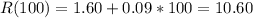
And for x = 100+k, for k positive, we have that the first 100 copies will cost as usual, but the remaining only will cost $0.06, thus
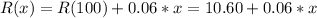
With this information we can conclude that

(Note that x should satisfy x≥0, otherwise the function woudlnt make sense)
b) The profit function p(x) can be obtained from R(x) by substracting the cost of making x copies, which is
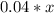 . This way, p(x) = R(x) -0.04x is given as follows
. This way, p(x) = R(x) -0.04x is given as follows