Question

In a one electron system, the probability of finding the electron within a shell of thickness ????rδr at a radius of rr from the nucleus is given by the radial distribution function, P(r)=r2R2(r)P(r)=r2R2(r) . An electron in a 1s1s hydrogen orbital has the radial wavefunction R(r)R(r) given by R(r)=2(1a0)3/2e−r/a0 R(r)=2(1a0)3/2e−r/a0 where a0a0 is the Bohr radius (52.9 pm)(52.9 pm) .

Calculate the probability of finding the electron in a sphere of radius 1.1a01.1a0 centered at the nucleus.

Answer 1

Explanation:

Solution:-

- The conclusions of Bohr's study have gave us hints regarding the probability of finding an electron ( e- ) in a 3 dimensional space of a nucleus.

- In Bohr's model the the 3-dimensional was considered as a spherical shell with thickness ( t = δr ) . Where ( r ) is the absolute radius of the density of electrons ( e - ) found in the vicinity of a nucleus.

- Bohr performed several experiments to determine what is the probability of finding of finding a single electron ( e- ) in a atom around its nucleus.

- He found that the probability P of finding an electron is a function of radial distance ( r )^2 - square of its distance from nucleus and the atom's wave-function R ( r ). The probability of the distribution is given as:

`P (r ) = r^2*R^2 ( r )`

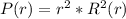
- Where R ( r ) is the wave-function specific for an atom. Here we will investigate an Hydrogen atom which has an orbital configuration = 1s orbitals.

`R ( r ) = 2*((1)/(a_o) )^(^(3)/(2)^) * e^(^-^(r)/(a_o)^)`

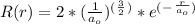
Where,
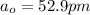`a_o = 52.9 pm` , is the Bohr's radius.

- We will determine the probability P ( r ) of finding that electron in a hydrogen atom at a radial distance r = 1.1a_o.

- Determine the P ( R ) by performing an integral from the center of spherical shell i.e nucleus r = 0 to r = 1.1a_o:

`P ( r ) = \int [ 2*((1)/(a_o) )^(^(3)/(2)^) * e^(^-^(r)/(a_o)^) ] ^2*r^2 dr\\\\P ( r ) = \int [ 4*((1)/(a_o) )^(^3^) * e^(^-^(2r)/(a_o)^) ] *r^2 . dr\\\\P ( r ) = 4*((1)/(a_o) )^(^3^) \int [ e^(^-^(2r)/(a_o)^) . r^2 ] . dr`

- Perform integration by parts:

`P ( r ) = 4*((1)/(a_o) )^(^3^) * ( [ (e^(^-^(2r)/(a_o)^) )/((-2)/(a_o) ) ]*r^2 - \int [ e^(^-^(2r)/(a_o)^) . 2r ] . dr)`

Answer 2

The question contains a typo error and with the help of the text editor I was able to put them down in the correct form. So, here is it.

In a one electron system, the probability of finding the electron within a shell of thickness
`\delta r` at a radius of r from the nucleus is given by the radial distribution function P (r) = r²R²(r)

An electron in a 1s hydrogen orbital has the radial wave function R(r) given by:

`R(r) = 2|(1)/(a_o)|^(3/2)} \ e ^(r/a_o)` where
`a__0` is the Bohr radius (52.9 pm)

Calculate the probability of finding the electron in a sphere of radius 1.1
`a__0`centered at the nucleus.

Answer:

Probability (P) ≅ 37.73 %

Explanation:

`\\ \\ \\Probability \ (P) = \int\limits^b_0 \ P({r}) \, \ dr \\ \\ \\ where \ b= 1.1a__0}} \\ \\ = \int\limits^b_0 r^2 \ 4 ((1)/(a__0)})^3 \ e^(-2r/a__0)} \ dr \\ \\ \\ = (4)/(a^3__0)}} \ \int\limits^b_r r^2 \ e^(-2r/a__0)} \ dr \\ \\ \\ = (4)/(a^3__0)}} [(r^2 (e^(-2r/a_0))/((-2/a_0_))}]^b___0}}} \ - \ \int\limits^b_0 2r (e^(-2r/a))/(-2/a_0) \ dr]`

`= (4)/(a__0)^3}[((a_0b^2e^(-2b/a_0))/((-2)))+a_0\int\limits^b_0 \ r \ e^(-2r/a) \ dr] -------- equation (1)`

However:

`\int\limits^b_0 \ r \ e^(-2r/a) \ dr \\ \\ \\ = [r \ (e^(-2r/a))/((-2/a))]^b__0}}- \int\limits^b_0 (e^(-2r/a))/((-2/a))} \\ \\ \\ = (ab \ e^(-2b/a))/((-2)) + (a)/(2) \ \int\limits^b_a \ e^(-2r/a) \ dr`

`= (ab \ e^(-2b/a))/((-2)) + (a)/(2) \frac {[e^(-2r/a)]^b_0}{(-2/a)}`

`\int\limits^b_0 \ r \ e^(-2r/a) \ dr = (ab \ e^(-2b/a))/((-2)) - (a^2)/(4)[e^(-2b/a)-1]`

Replacing the value of
`\int\limits^b_0 \ r \ e^(-2r/a) \ dr` into equation (1); we have:

`Probability (P) = (4)/(a__0)^3}[((a_0b^2e^(-2b/a_0))/((-2)))+ (ab \ e^(-2b/a))/((-2)) - (a^2)/(4)[e^(-2b/a)-1]]`

Substituting b = 1.1
`a__0` ; we have:

`Probability (P) = (4)/(a^3)[((a^3(1.1)^2e^(-2(1.1)))/((-2)))+ {a^2_3(1.1) \ e^(-2*1.1)} - (a^3)/(4)[e^(-2(1.1))-1]]`

Probability (P) = 4 (-0.067036 - 0.06094 + 0.222299)

Probability (P) = 0.377292

Probability (P) ≅ 37.73 %