{Hello, arman78624}
Answer:
12.5%
Explanation:
Since it given that the length of the sie of a square A is 50% of the length of the side of square B. As well as given us the question we need to find the answer to which is:
Express the area of the shaded region of square A as a percentage of the area of square B.
What we need:
Area of shaded region of Square A as a % of Area of Square B
Now we can solve but first :
Let "b" be the side length of Square B
Let "a" be the side length of Square A
As well as:
It given side length of Square A (a) = 50% (1/2) of side length of Square B (b), therefore we have,
a = ½b
Area of a square = s², where s is the side length
Area of Square A = (½b)² = b²/4
Area of Square B = b²
Finding the area of the shaded region of the Square A = ½ of area of Square A.
Area of shaded region of Square A = ½*(b²/4) = b²/8
Expressing the area of the shaded portion of square A as a percentage of are of Square B:
Area of shaded portion of Square A ÷ Area of Square B × 100%
Solving:
⇒
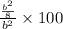
⇒
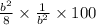
⇒
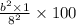
⇒
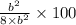
⇒

Base on the solving above we can conclude that:
The area of the shaded region of Square A is 12.5% of the area of Square B.
~[DiscordUser]~