Question

3. Zircon crystals in the Igneous Sill have a ratio of 91.7% Uranium-238 to 8.3% Lead-206. (1 point) What is the age of the Igneous Sill? _____________

Answer 1

`t = 558791705.6\,years`

Step-by-step explanation:

After reading the statement of the problem, part of the initial mass of Uranium-238 has become into Lead-206. The decayment of the isotope is modelled by the following expression:

`(m)/(m_(o)) = e^{-(t)/(\tau) }`

The Uranium-238 has a half-life of 4.47 billion years and the time constant as function of the half-life is:

`\tau = (t_(1/2))/(\ln 2)`

`\tau = (4.47* 10^(9)\,years)/(\ln 2)`

`\tau = 6.449* 10^(9)\,years`

The age of the Igneous Sill is found by clearing the variable in the decayment equation:

`\ln (m)/(m_(o)) = -(t)/(\tau)`

`t = - \tau \cdot \ln (m)/(m_(o))`

`t = - (6.449* 10^(9)\,years)\cdot \ln 0.917`

`t = 558791705.6\,years`

Answer 2

The age of the Igneous Sill is 1.456 × 10¹⁰ years

Step-by-step explanation:

The radioactive decay is given as follows;

`U_t = U_0 e^(-\lambda t)`

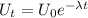
Also, where 1 Uranium 238 atom disintegrates to produce 1 Lead 206 atom, we write;

`U_t = (U_t + Pb_t) e^(-\lambda t)`

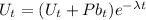
Such that;

`(Pb_t)/(U_t) = e^(-\lambda t) - 1`

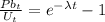
The decay constant, λ is given by the following;

`\lambda = (0.693)/(4.468 * 10^9) = 1.55 * 10^(-10) \ year^(-1)`

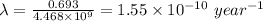
Percentage by mass of Uranium = 91.7%

Percentage by mass of Uranium = 8.3%

Number of moles of Uranium 238 and Lead 206 present is therefore;

`nPb_t = (8.3)/(205.974 465) = 0.0403`

`nU_t = (91.7)/(238.05078826) = 0.385`

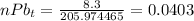
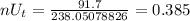
Therefore we have;

`(0.0403)/(0.385) = e^(-\lambda t) - 1 = e^{-1.55 * 10^(-10) * t} - 1= 0.1046`

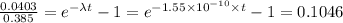
From which t is found to be t = 14555074285.2 = 1.456 × 10¹⁰ years.