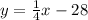Question

Write the equation of a line in slope-intercept form that is parallel to the given line and passes through the point (12,-25). Y=1/4x+2

Answer 1

Answer: y=1/4x-28

Explanation:

Answer 2

Given:

The given equation of the line is
`y=(1)/(4)x+2`

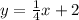
The line that is parallel to the given line passes through the point (12,-25)

We need to determine the equation of the line.

Slope:

Since, the two lines are parallel, then their slope must be same.

Thus, from the equation
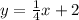`y=(1)/(4)x+2`, the slope is given by

`m=(1)/(4)`

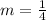
Thus, the slope of the parallel line is
`m=(1)/(4)`

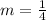
Equation of the line:

The equation of the line can be determined using the formula,

`y-y_1=m(x-x_1)`

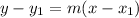
Substituting the slope and the point (12,-25), we have;

`y+25=(1)/(4)(x-12)`

`y+25=(1)/(4)x-3`

`y=(1)/(4)x-28`

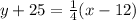
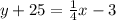
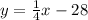
Thus, the equation of the line is
`y=(1)/(4)x-28`