Answer: The determinant is smaller than zero. (b^2 - 4ac < 0.)
Explanation:
For a quadraitc equation of the shape:
ax^2 + bx + c
We have that the roots (the points where the graph intercepts the x-axis) can be found by the Bhaskara's function:
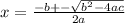
The term inside the square root is called the determinant.
D = b^2 - 4ac
if we have D < 0, then we will have a square root of a negative number, this means that we will have an imaginary number.
If we have imaginary solutions, then we do not have real roots, which means that the graph never intersects the x-axis.
The conclusion is that, if the graph does not intercept the x-axis, then:
b^2 - 4ac < 0.