Question

Math problem help me

Answer 1

`y=3x+2`

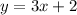
Explanation:

To find the equation, use the slope-intercept formula:

`y=mx+b`

m is the slope and b is the y-intercept. Now, it'll really help to draw a line through the points, connecting them. If you look at point (0,2), we can see that this is the y-intercept (where a point sits on the y-axis when x=0). You can insert this into the equation by taking the y value:

`(0,2)\\y=mx+2`

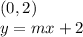
Now, take any two points to find the slope. To make it easier, I'll use (1,5) and (0,2). Use the slope formula for when you know two points:

`(y(2)-y(1))/(x(2)-(x1)) =(rise)/(run)`

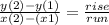
Rise over run is the change in the y-axis over the change in the x-axis. Insert values:

`(1(x1),5(y1))\\(0(x2),2(y2))\\\\(2-5)/(0-1)`

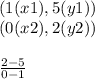
Solve:

`(2-5)/(0-1)=(-3)/(-1)`

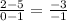
Since both are negative, the result is a positive:

`(-3)/(-1)=(3)/(1) =3`

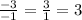
Insert this into the equation as m, the slope:

`y=3x+2`

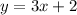
Done.