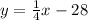Answer:
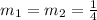
And then since the new equation have the following form:
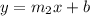
We can use the point given (x=12, y = -25) in order to find the intercept with this equation:
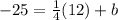
And solving for the intercept b we got:

We subtract in both sides 3 and we got:
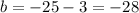
And our final equation who satisfy the condition given is:
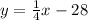
Explanation:
For this case we have the following equation given:
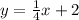
And we want to find an equation of a line parallel to the given function and this case we need to satisfy this condition:
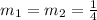
And then since the new equation have the following form:
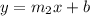
We can use the point given (x=12, y = -25) in order to find the intercept with this equation:
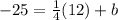
And solving for the intercept b we got:

We subtract in both sides 3 and we got:
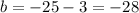
And our final equation who satisfy the condition given is: