Question

The mean score on a science assessment for 59 male high school students was 319.5 and the standard deviation 2.5. The mean test score on the same test for 40 female high school students was 298.9 and the standard deviation was 1.2. For this assessment, the population standard deviation for males is σ = 2.3 and the population standard deviation for females is σ = 2.0. At a = 0.02 , can you support the claim that mean scores on the science assessment for male high school students were higher than for the female high school students?

Answer 1

`z=\frac{(319.5-298.9)-0}{\sqrt{(2.3^2)/(59)+(2.0^2)/(40)}}}=47.302`

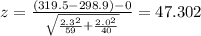
Thsis value is very high and if we find the p value we would get:

`p_v= P(z>47.302) \approx 0`

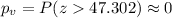
So then we have enough evidence to support the claim that the true mean for males is higher than the true mean for females.

Explanation:

Data given and notation

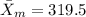`\bar X_(m)=319.5` represent the mean for the sample male

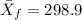`\bar X_(f)=298.9` represent the mean for the sample female

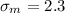`\sigma_(m)=2.3` represent the population standard deviation for the males

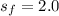`s_(f)=2.0` represent the population standard deviation for the females

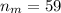`n_(m)=59` sample size for the group male

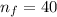`n_(f)=40` sample size for the group female

z would represent the statistic (variable of interest)

System of hypothesis

We need to conduct a hypothesis in order to check if that mean scores on the science assessment for male high school students were higher than for the female high school students, the system of hypothesis would be:

Null hypothesis:
`\mu_(m)-\mu_(f) \leq 0`

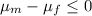
Alternative hypothesis:
`\mu_(m) - \mu_(f)> 0`

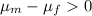
The staistic for this case is:

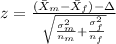`z=\frac{(\bar X_(m)-\bar X_(f))-\Delta}{\sqrt{(\sigma^2_(m))/(n_(m))+(\sigma^2_(f))/(n_(f))}}` (1)

With the info given we can replace in formula (1) like this:

`z=\frac{(319.5-298.9)-0}{\sqrt{(2.3^2)/(59)+(2.0^2)/(40)}}}=47.302`

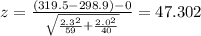
Thsis value is very high and if we find the p value we would get:

`p_v= P(z>47.302) \approx 0`

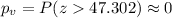
So then we have enough evidence to support the claim that the true mean for males is higher than the true mean for females.