Answer:
The percentage of the bag that should have popped 96 kernels or more is 2.1%.
Explanation:
The random variable X can be defined as the number of popcorn kernels that popped out of a mini bag.
The mean is, μ = 72 and the standard deviation is, σ = 12.
Assume that the population of the number of popcorn kernels that popped out of a mini bag follows a Normal distribution.
Compute the probability that a bag popped 96 kernels or more as follows:
Apply continuity correction:
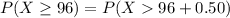
*Use a z-table.
The probability that a bag popped 96 kernels or more is 0.021.
The percentage is, 0.021 × 100 = 2.1%.
Thus, the percentage of the bag that should have popped 96 kernels or more is 2.1%.