Question

Men’s heights are normally distributed with a mean of 72.1 inches and a standard deviation of 3.6 inches. A social organization for short people has a requirement that men must be at most 64 inches tall. What percentage of men meet this requirement? Choose the correct answer:

Answer 1

The percentage of men meet the social organization for short people's requirement is 0.842%.

Explanation:

The random variable X can be defined as the height of men.

The random variable X is normally distributed with mean, μ = 72.1 inches and standard deviation, σ = 3.6 inches.

It is provided that a social organization for short people has a requirement that men must be at most 64 inches tall.

Compute the value of P (X ≤ 64) as follows:

Apply continuity correction:

P (X ≤ 64) = P (X < 64 - 0.50)

= P (X < 63.50)

`=P((X-\mu)/(\sigma)<(63.5-72.1)/(3.6))`

`=P(Z<-2.39)\\=0.00842`

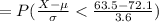
*Use a z-table for the probability.

The percentage is, 0.00842 × 100 = 0.842%.

Thus, the percentage of men meet the social organization for short people's requirement is 0.842%.