Question

Find the volume of the composite figure to the nearest tenth. Use 3.14 for pi.

Answer 1

Given:

In the given fig,

The radius of the cylinder = 15 ft

The height of the cylinder = 26 ft

The height of the cone = 21 ft

The radius of the cone = 15 ft

To find the volume of the cone, the volume of the cylinder and the composite figure.

Formula

The volume of the given composite fig is

`V = V_(1) +V_(2)`

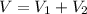
where,
`V_(1)` be the volume of the cone.

`V_(2)` be the volume of the cylinder.

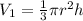`V_(1) = (1)/(3) \pi r^(2) h`, r be the radius and h be the height.

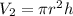`V_(2) = \pi r^(2) h`, r be the radius and h be the height.

Now,

Putting, r = 15, h = 21 and π = 3.14 we get,

`V_(1) = (1)/(3) (3.14)(15^(2) )(21)` cube ft

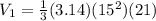`V_(1) = 4945.5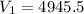` cube ft

Again,

Putting,

`V_(2) = (3.14)(15^(2) )(26)` cube ft

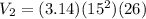`V_(2) = 18369` cube ft

Therefore, the volume of the composite fig = (4945.5+18369) cube ft = 23314.5 cube ft

Hence,

a) The volume of the cone is 4945.5 cube ft.

b) The volume of the cylinder is 18369 cube ft.

c) The volume of the composite figure is 23314.5 cube ft.