Question

Cesium-135 has a half life of approximately 30 years. If a sample, which originally contained 8 mg, is found to contain 0.25 mg of Cs-135, how old is the sample?

____ half-life have occurred so the sample is ___ hours.

Answer 1

The sample has 150 years, 1314000 hours

Step-by-step explanation:

The element decay follows the first order kinetics law:

ln[Cs-135] = -kt + ln [Cs-135]₀ (1)

Where [Cs-135] is concentration after t time, k is rate constant in time, and [Cs-135]₀ is initial concentration

Half-life formula is:

`t_(1/2) = (ln2)/(k)`

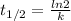
30 years = ln2 / k

k = 0.0231 years⁻¹

Using rate constant in (1):

ln[0.25mg] = -0.0231 years⁻¹×t + ln [8mg]

-3.466 = -0.0231 years⁻¹×t

150 years = t

The sample has 150 years

In hours:

150years × (365days / 1year) × (24hours / 1day) = 1314000 hours