Question

What is the equation of the line of best fit for the following data? Round the

slope and y-intercept of the line to three decimal places.
A. y = 0.894x + 0.535
B. y = -0.894x + 0.535
c. y=0.535x+0.894
D. y= -0.535x + 0.894

Answer 1

Answer: A

Explanation:

Answer 2

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=438-(44^2)/(5)=50.8`

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)=415-(44*42)/(5)=45.4`

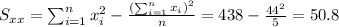
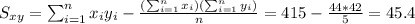
And the slope would be:

`m=(45.4)/(50.8)=0.8937 \approx 0.894`

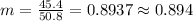
Now we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(44)/(5)=8.8`

`\bar y= (\sum y_i)/(n)=(42)/(5)=8.4`

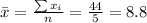
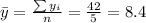
And we can find the intercept using this:

`b=\bar y -m \bar x=8.4-(0.894*8.8)=0.535`

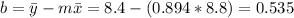
So the line would be given by:

`y=0.894 x +0.535`

And the best option is:

A. y = 0.894x + 0.535

Explanation:

We have the following dataset given

x: 5,6,9,10,14

y: 4,6,9,11,12

We want to find the least-squares line appropriate for this data given by this general expresion:

`y = mx +b`

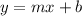
Where m is the slope and b the intercept

For this case we need to calculate the slope with the following formula:

`m=(S_(xy))/(S_(xx))`

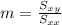
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

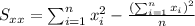
So we can find the sums like this:

`\sum_(i=1)^n x_i = 44`

`\sum_(i=1)^n y_i =42`

`\sum_(i=1)^n x^2_i =438`

`\sum_(i=1)^n y^2_i =398`

`\sum_(i=1)^n x_i y_i =415`

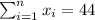
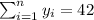
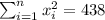
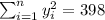
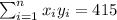
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=438-(44^2)/(5)=50.8`

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)=415-(44*42)/(5)=45.4`

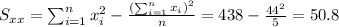
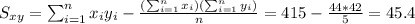
And the slope would be:

`m=(45.4)/(50.8)=0.8937 \approx 0.894`

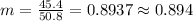
Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(44)/(5)=8.8`

`\bar y= (\sum y_i)/(n)=(42)/(5)=8.4`

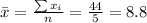
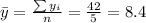
And we can find the intercept using this:

`b=\bar y -m \bar x=8.4-(0.894*8.8)=0.535`

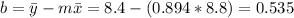
So the line would be given by:

`y=0.894 x +0.535`

And the best option is:

A. y = 0.894x + 0.535