Question

What is the solution to the system of equations?

Negative 6 x minus two-fifths y = 8
One-half x + 3 y = 29

(10, –2)
(10, 2)
(2, 10)
(–2, 10)

Answer 1

(-2, 10)

Explanation:

Our equations are:

-6x -
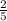`(2)/(5)`y = 8

`(1)/(2)`x + 3y = 29

Let's multiply the second equation by 12:

12 * (
`(1)/(2)`x + 3y) = 12 * 29

6x + 36y = 348

Now, add this new equation to the first equation:

6x + 36y = 348

+ -6x -
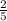`(2)/(5)`y = 8

_______________

(36 - 2/5)y = 356

36 - 2/5 = 180/5 - 2/5 = 178/5

Divide both sides by 178/5:

y = 356 / (178/5) = 356 * (5/178) = 10

Plug this back into one of the original equations to get x:

(1/2)x + 3y = 29

(1/2)x + 3 * 10 = 29

(1/2)x = -1

x = -2

The answer is (-2, 10).

Hope this helps!

Answer 2

D) (-2,10)

Explanation:

Negative 6 x minus two-fifths y = 8

-6x - (2/5)y = 8

One-half x + 3 y = 29

(1/2)x + 3y = 29

(1/2)x = 29 - 3y

x = 58 - 6y

-6(58 - 6y) - (2/5)y = 8

-348 + 36y - (2/5)y = 8

356 = 35.6y

y = 10

x = 58 - 6(10) = -2

(-2, 10)