Given:
A square pyramid with a base edge length of 8 m and a slant height of 12 m.
To find:
The height of the pyramid.
Solution:
A right-angled triangle can be formed with the slant height, the height, and half the length of the base edge.
The slant height of the pyramid is 12 m long and is the hypotenuse of the right-angled triangle.
Assume the height of the pyramid is x and half the length of the base edge is
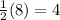 m.
m.
According to the Pythagorean theorem, the square of the hypotenuse will be equal to the sum of the squares of the other two sides.
The hypotenuse measures 12 m while the other two sides measure 4 m and x m each.
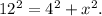
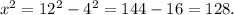
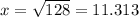 m.
m.
The height of the square-based pyramid is 11.313 m.