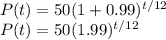Question

Nicholas sent a chain letter to his friends, asking them to forward the letter to more friends. Every 12

weeks, the number of people who receive the email increases by an additional 99%, and can be modeled
by a function, P, which depends on the amount of time, t (in weeks).
Nicholas initially sent the chain letter to 50 friends.
Write a function that models the number of people who receive the email t weeks since Nicholas initially
sent the chain letter.
P(t) =?

Answer 1

`P(t)=50(1.99)^(t/12)`

Explanation:

The problem can be modeled by using the compound growth formula.

Given, Initial number
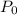`P_0` of people who Nicholas sent the chain letter to=50

The growth rate, r =99%=0.99

Period of Growth,k =12 Weeks

`P(t)=P_0(1+r)^(t/k)`

Therefore, in any week (t) after Nicholas initially sent the mail, the number of people who receive the email is modeled by the function:

`P(t)=50(1+0.99)^(t/12)\\P(t)=50(1.99)^(t/12)`