Answer:
(A)The northern lighthouse is 8.2 miles closer than the southern lighthouse.
Explanation:
The triangle attached represents the given problem.
First, let us determine the distance of the Boat from each of the lighthouse.
In Triangle ABC,
∠A+∠B+∠C=180 degrees
21+∠B+16=180
∠B=180-37=143 degrees.
Using Law of Sines
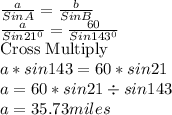
Similarly
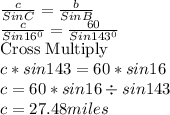
Difference in Distance =35.73-27.48=8.25 miles
Therefore, the northern lighthouse is 8.2 miles closer than the southern lighthouse.