Answer:
Mr.Pratt can select three students to win these awards in 2,600 ways.
Step-by-step explanation:
In mathematics, the procedure to select k items from n distinct items, without replacement, is known as combinations.
The formula to compute the combinations of k items from n is given by the formula:
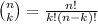
Mr. Pratt has three prizes to give away.
The total number of students in his class is, n = 26.
He has k = 3 prizes, namely a pencil, an eraser, and a homework pass.
Compute the number of combinations of three students Mr. Pratt can select from 26 students to give away the prizes as follows:
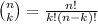
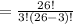

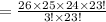
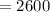
Thus, Mr.Pratt can select three students to win these awards in 2,600 ways.