Answer: 11.40
Explanation:
For this question you would use the Pythagorean Theorem:
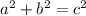
First, let's create a triangle between points V, U, and also the center (we'll mark the center point O)
So now we have a triangle VOU
Pythagorean Theorem states that to find the hypotenuse, c, we must take the sum of the square of a and b.
Let a be the length VO and let b be the length OU
VO (a) = 9
OU (b) = 7
Now take the formula and plug in the values to find c
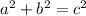
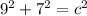
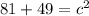
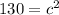
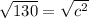

Therefore we can see that length VU is 11.40 long