Question

Y=4x ² can you help me solve it show me how to do it

Answer 1

Vertex: (0, 0)

Focus: (0,
`(1)/(16)`)

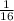axis of symmetry:
`x` = 0

Directrix:
`y` =
`-(1)/(16)`

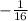
solution(s):
`x` = 0

Explanation:

Vertex:

The equation for a parabola is y = a(x - h)² + k

the vertex is the point (h, k), so in this equation the vertex is (0, 0)

Focus:

The equation for the focus of a vertical parabola is 4p(y - k) = (x - h)²

(p is the distance from the vertex to the parabola)

axis of symmetry:

The axis of symmetry is a vertical line that divides the parabola into two equal halves.

In this instance, because the vertex is (0, 0), the axis of symmetry is
`x` = 0

Directrix:

The directrix is the point that is an equally far from the vertex as the focus is. Because this is the case, it would be the opposite of the focus, making the directrix
`-(1)/(16)`

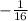
Solution:

The only solution is
`x` = 0 because the parabola only touches the x-axis once at the vertex