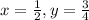Answer:
Explanation:
Given:
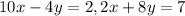
To find: points of intersection of the given lines
Solution:
In substitution method, the system of equations is solved by expressing one variable in terms of another, as a result, removing one variable from an equation.
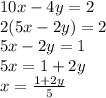
Put
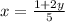 in the equation
in the equation
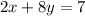
![2x+8y=7\\2[(1+2y)/(5)]+8y=7\\ 2+4y+40y=35\\44y=35-2\\44y=33\\y=(33)/(44)\\ =(3)/(4)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/69w8i5iiw5m6yapt4in8sgpjoy1tq994kg.png)
Put
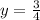 in the equation
in the equation
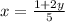
![x=(1+2y)/(5)\\=(1)/(5)[1+2((3)/(4))]\\=(1)/(5)[1+((3)/(2))]\\\\=(1)/(5)((2+3)/(2)) \\\\=(1)/(5)((5)/(2))\\\\=(1)/(2)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/6snnyefczmmksxas9e2tar57115r348na3.png)
Therefore,