Question

A reporter surveyed 300 randomly selected people of all ages about their opinion of a new song. The results are shown in the table below.

survey

Which of the following is a valid conclusion about the data? Select ALL that apply.

Question 1 options:

Most people had no opinion about the new song.


Of the people who liked the song, more than half of them were between the ages of 25-46.


People who did not like the song were more likely to be older than age 46


The people who had no opinion were most likely to be younger than 25 years old.


70% of the people who were younger than 25 either liked the new song or had no opinion.

Answer 1

HUH is 3 and 5

Explanation:

Answer 2

Options (3) and (5) are correct.

Explanation:

The total number of people selected is, N = 300.

The probability of an event E is the ratio of the number of favorable outcomes to the total number of outcomes.

`P(E)=(n(E))/(N)`

Consider the probability distribution table attached below.

• Considering opinion as a factor, it can be seen from the probability table that the probability of people liking the song is more than the other opinions. So, it can be concluded that most people liked the song.

• Compute the probability of people between ages 25-46 liking the song as follows:

`P(25-46|Like)=(P(25-46\ \cap\ Like))/(P(Like))=(0.167)/(0.457)=0.365`

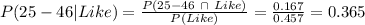
So, less than half of the people who liked the song were of ages

25-46.

• From the probability table it can be seen that the probability of people who did not liked the song and were older than 46 is more than the other age groups. Thus, it can be said that people who did not like the song were more likely to be older than age 46.

• From the probability table it can be seen that the probability of people who had no opinion is more in the age group 25-46. Thus, it can be said that the people who had no opinion were not most likely to be younger than 25 years old.
• The event of liking the song and having no opinion are mutually exclusive.

Compute the probability of people who were younger than 25 either

liking the new song or having no opinion as follows:

`P(Like\ \cup\ No\ opinion)=P(Like)+P(No\ opinion)\\=(0.183+0.050)/(0.333)\\=0.699\\\approx0.70\\`

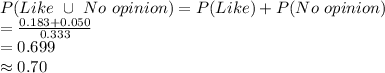
Thus, it can be said that 70% of the people who were younger than 25

either liked the new song or had no opinion.

Thus, options (3) and (5) are correct.