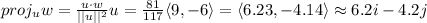Determine the projection of w onto u

Question

asked Dec 3, 2021 67.0k views

2 Answers

Boris Gorelik · Answer 1 · 2021-12-07T20:59:51+0000

Answer:

c. 6.2i - 4.2j

Explanation:

The vector projection when the angle θ not known can be calculated using the following property of the dot product:

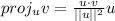
$proj_uv=(u\cdot v)/(||u||^2) u$

Where the dot product of two vectors is given by:

$u\cdot v= $$\sum_(i=1)^(n) u_iv_i= u_1v_1+u_2v_2+...+u_nv_n$$$

And the magnitude of a vector is given by:

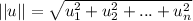
||u||=√(u_1^2+u_2^2+...+u_n^2)

Using the previous definition, let's calculate the projection of w onto u:

First let's calculate the dot product between w and u:

$u\cdot w =(9*19)+(-6*15)=171-90=81$

Now let's find the magnitude of u:

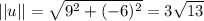
||u||=√(9^2+(-6)^2) = 3 √(13)

So:

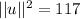
||u||^2=117

Therefore:

$proj_uw=(u\cdot w)/(||u||^2) u=(81)/(117) \langle9,-6\rangle=\langle6.23,-4.14\rangle\approx6.2i-4.2j$