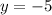Answer:
x = -2, y = -5
Explanation:
Isolate x for 3x - 2y = 4
3x - 2y = 4
Add 2y to both sides
3x -2y + 2y = 4 + 2y
Simplify
3x = 4 + 2y
Divide both sides by 3
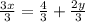
Simplify
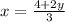
Now we substitute
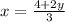 for x in 4x - 3y = 7
for x in 4x - 3y = 7
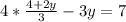
Isolate y for
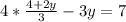
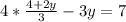
Expand
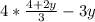
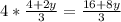
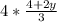
Multiply fractions:
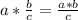
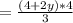
Expand
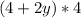
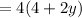
Apply the distributive law:
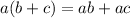
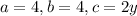
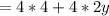
Simplify
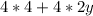
Multiply the numbers:
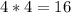
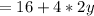
Multiply the numbers:
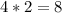
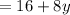
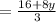
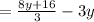
Convert element to fraction:
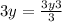
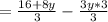
Since the denominators are equal, combine the fractions:
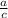 ±
±
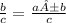
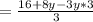
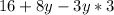
Multiply the numbers:
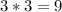
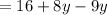
Add similar elements:
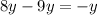
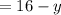
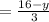
Apply the fraction rule:
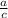 ±
±
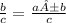
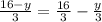
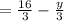
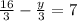
Multiply both sides by 3
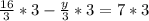
Simplify
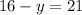
Subtract 16 from both sides
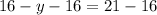
Simplify
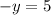
Divide both sides by -1
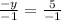
Simplify
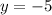
For
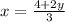 substitute
substitute
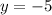
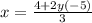
Remove parentheses:
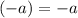
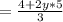
Multiply the numbers:
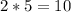

Subtract the numbers:
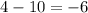

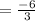
Apply the fraction rule:
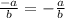
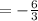
Divide the numbers:
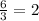

The solutions to the system of equations are
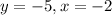
Checking answers
Plug in
 and
and
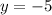 into
into
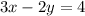 and
and
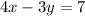
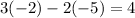
Remove parentheses:
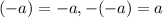
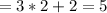
Multiply the numbers:
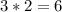
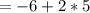
Multiply the numbers:
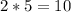
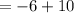
Add/subtract the numbers:
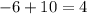
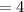
First equation proven true
Substitute the values of x and y into the second equation
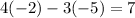
Follow the PEMDAS order of operations
Multiply and divide left to right
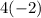
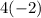
Apply rule
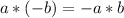
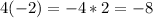


Multiply and divide left to right
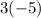
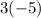
Apply rule
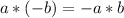
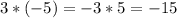
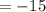

Add and subtract left to right
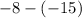
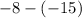
Apply rule
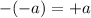
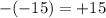
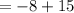
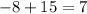
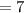
Second equation proven true.
Both equations are true with
 and
and