Answer:
The probability that a person surveyed was either male or had a cell phone is 0.775.
Explanation:
Denote the events as follows:
M = a person is male
F = a person is female
X = a person has a cell phone
Y = a person does not have a cell phone
The information provided is:
N = 800
n (M) = 420
n (X) = 325
n (X ∩ F) = 200
The remaining data is computed as follows:
M F Total
X 125 200 325
Y 295 180 475
Total 420 380 800
The probability of the union of two events is given by:
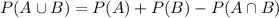
Compute the probability of selecting a male as follows:

Compute the probability that a person had a cell phone as follows:

Compute the probability that a person is male and had a cell phone as follows:
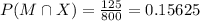
Compute the probability that a person surveyed was either male or had a cell phone as follows:

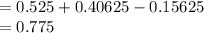
Thus, the probability that a person surveyed was either male or had a cell phone is 0.775.