Question

Assume that you want to test the claim that the paired sample data come from a population for which the mean difference is µd = 0. Compute the value of the t test statistic. Round intermediate calculations to four decimal places as needed and final answers to three decimal places as needed.x: 34 39 28 33 27 23 35 33y: 32 35 34 33 28 28 35 32a. t = -0.523b. t = -1.480c. t = 0.690d. t = -0.185

Answer 1

d: 2, 4, -6, 0, -1, -5, 0, 1

The second step is calculate the mean difference

`\bar d= (\sum_(i=1)^n d_i)/(n)= (29)/(8)=-0.625`

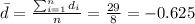
The third step would be calculate the standard deviation for the differences, and we got:

`s_d =(\sum_(i=1)^n (d_i -\bar d)^2)/(n-1) =3.378`

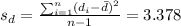
The next step is calculate the statistic given by :

`t=(\bar d -0)/((s_d)/(√(n)))=(-0.625 -0)/((3.378)/(√(8)))=-0.523`

And the correct option would be:

a. t = -0.523

Explanation:

We assume the following notation:

x=test value after , y = test value before

x: 34 39 28 33 27 23 35 33

y: 32 35 34 33 28 28 35 32

The system of hypothesis for this case is given by:

Null hypothesis:
`\mu_y- \mu_x = 0`

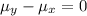
Alternative hypothesis:
`\mu_y -\mu_x \\eq 0`

The first step is calculate the difference
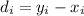`d_i=y_i-x_i` and we obtain this:

d: 2, 4, -6, 0, -1, -5, 0, 1

The second step is calculate the mean difference

`\bar d= (\sum_(i=1)^n d_i)/(n)= (29)/(8)=-0.625`

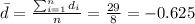
The third step would be calculate the standard deviation for the differences, and we got:

`s_d =(\sum_(i=1)^n (d_i -\bar d)^2)/(n-1) =3.378`

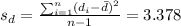
The next step is calculate the statistic given by :

`t=(\bar d -0)/((s_d)/(√(n)))=(-0.625 -0)/((3.378)/(√(8)))=-0.523`

And the correct option would be:

a. t = -0.523