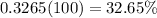Question

A target with a diameter of 70 cm has 4 scoring zones formed by concentric circles. The diameter of the center circle is 10 cm. The width of each ring is 10 cm. A dart hits the target at a random point. Find the probability that it will hit a point in the blue region.

Answer 1

0.490, ur welcome, that other guy was capping

Explanation:

Answer 2

`32.65\%`

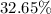
Explanation:

see the attached figure to better understand the problem

we know that

The probability that it will hit a point in the blue region is equal to divide the area of the blue ring by the total area of the target

step 1

Find the area of the blue ring

The radius of the blue ring is
`(5+10+10)=25\ cm`

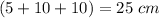
The radius of the red ring is
`(5+10)=15\ cm`

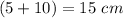
The area of the blue ring is given by the formula

`A=\pi(25^2-15^2)`

`A=400\pi\ cm^2`

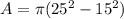
step 2

Find the total area of the target

The radius of the target is

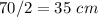`70/2=35\ cm` ---> the radius is half the diameter

`A=\pi (35^(2)]\\A=1,225\pi\ cm^(2)`

step 3

Find the probability

`(400\pi)/(1,225\pi)= 0.3265`

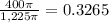
Convert to percentage

Multiply by 100

`0.3265(100)=32.65\%`