Answer:
~91 chirps/min
Explanation:
This exercise is asking us to estimate based on the values in the table. If we know the temperature is 65°F, let's find the closest values given to interpolate (assuming the data is fairly linear, which it appears to be).
Looks like the closest ones are 60° and 68°. We will look at their corresponding chirps/min and guess a number in between those two.
60° -> 81 chirps/min
68° -> 97 chirps/min
Because 65 is closer to 68 than 60, we expect our result to be closer to 97 than 81.
slope = rise/run
 =
=
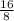 = 2 chirps/min/°F. So for every °F increase, we expect to increase by 2 chirps/min.
= 2 chirps/min/°F. So for every °F increase, we expect to increase by 2 chirps/min.
60+5 = 65, so let's add 2*5 = 10 chirps/min to 60 to get 91 chirps/min. This corresponds with what we would have guessed.