Question

“angle A = 32, AC = 9, BC = x. Find x to two decimal places, don’t forget to round properly based on the third decimal place.” Pls answer & explain thanks

Answer 1

Given:

Given that ABC is a right triangle.

The measure of ∠A is 32°.

The length of AC is 9 units.

The length of BC is x units.

We need to determine the value of x.

Value of x:

The value of x can be determined using the trigonometric ratio.

Thus, we have;

`sin \ \theta=(opp)/(hyp)`

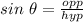
where θ = A, the side opposite to A is BC and hypotenuse is AC.

Thus, we have;

`sin \ A=(BC)/(AC)`

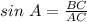
Substituting BC = x and AC = 9, we get;

`sin \ 32=(x)/(9)`

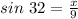
Multiplying both sides by 9, we have;

`sin \ 32 * 9=x`

`4.77=x`

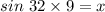
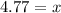
Thus, the value of x is 4.77 units.