Given:
The length of the side of the metal is x + 7.
The length of the side of the hole is x - 2.
We need to determine the area of the metal part or the shaded region.
Area of the metal:
The area of the metal can be determined using the formula,
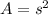
Substituting s = x + 7, we get;
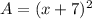
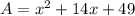
Thus, the area of the metal is
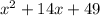 square units.
square units.
Area of the hole:
The area of the hole can be determined using the formula,
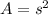
Substituting s = x -2 ,we get;
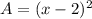
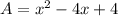
Thus, the area of the hole is
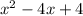 square units.
square units.
Area of the shaded region:
The area of the shaded region can be determined by subtracting the area of the hole from the area of the metal.
Thus, we have;
Area = Area of the metal - Area of the hole
Substituting the values, we have;
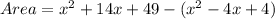
Simplifying, we have;
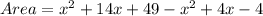
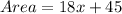
Thus, the area of the shaded region is (18x + 45) square units.