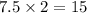Question

If the hypotenuse of a 30-60-90 triangle has length 15, then the shorter leg has length

5.5

6.5

7.5

Answer 1

Explanation:

Given : If the hypotenuse of a 30-60-90 triangle has length 15 then the shorter leg has length 5.5 , 6.5 , 7.5.

To find : What is the length of the other leg and hypotenuse ?

Solution :

For a 30-60-90 triangle, sides are in the ratio
`1:√(3):2`

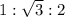
where, 1 is the shorter side,

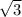`√(3)` the other side

and 2 the hypotenuse.

Short leg = 5.5

Other leg =
`5.5* \sqrt3=5.5\sqrt3`

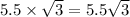
Hypotenuse =
`5.5* 2=11`

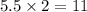
Short leg = 6.5

Other leg =
`6.5* \sqrt3=6.5\sqrt3`

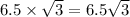
Hypotenuse =
`6.5* 2=13`

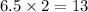
Short leg = 7.5

Other leg =
`7.5* \sqrt3=7.5\sqrt3`

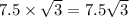
Hypotenuse =
`7.5* 2=15`