Answer:
B) It decreases 22% per year.
Explanation:
We are given that The value, v(.r), of his portfolio can be modeled with the function :
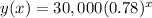
Where x is the number of years since he made his investment.
Formula :
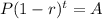
Where P = Principal
r = rate of decrease
t = time
A = Amount after t years
So, On comparing
P = 30000
t=x
A=y(x)
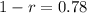
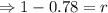
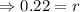
So, r = 0.22
r=22%
So, Rate of decrease is 22%
So, Option B is true,
It decreases 22% per year.