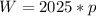Question

(1 point) A rectangular tank that is 3 feet long, 6 feet wide, and 15 feet tall is filled with a liquid that has a density of p pounds per cubic foot. If a spout is connected to the top of the tank, how much work will it take to pump all of the liquid out of the tank through the spout?

Answer 1

Hence the work done by the pumping the liquid with density p is 2025*p

Explanation:

Given:

Rectangular tank with dimensions as 3 feet long,6 ft wide and 15 ft tall.

liquid with p density is taken out of tank.

To Find:

Work done during taking out liquid

Solution:

Using the work as integral ,calculate the work function and with given limits to the function.

So

Now consider Area of section by which the liquid is going to pumped out of tank,

Area of cross section=length * width

Here l=3-ft and w=6-ft

Area of cross section=18 sq ft

Using definition for work,

Work=force* displacment

Consider dy be displacement along the height (15 ft tall tank)

And ,

force =Area * density

force=18*p

Hence ,Work=18*p*dy

Here the limits is starting from 0 to 15 ft

So ΔW=
`\int\limits^a_b {18*p} \, dy`

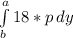
here a=0 and b=15

Now integrating of both sides we get,

`W=18*p[y^2/2] over the limits 0 to 15`

`W=18*p[225/2]`

`W=2025*p`